Как готовиться к ЕГЭ по математике
_780.jpg)
ЕГЭ по математике решает, на какие вузы и специальности реально подать документы, особенно если нужен профиль. Материал объёмный, времени часто мало, поэтому нужен чёткий план, а не хаотичные варианты из интернета.
Дальше разбирается, как готовиться к базовой и профильной математике с прицелом на профиль: какие темы учить в первую очередь, как выстроить подготовку на год, полгода или пару месяцев и какие задания проработать, чтобы выйти на нужный балл.
Зачем нужна математика на ЕГЭ и чем она отличается от школьной
Математика на ЕГЭ определяет, откроются ли технические, инженерные, ИТ‑, экономические и многие естественно‑научные направления. Для части гуманитарных специальностей достаточно базового уровня, но для конкуренции на бюджет по популярным программам почти всегда требуют профиль.
Школьная математика ориентирована на поурочную проверку тем и контрольные с подсказками учителя. ЕГЭ же — единый вариант для всех, жёсткий лимит времени, отсутствие калькулятора и готовых формул, задания по кодификатору с типовыми ловушками и строгими критериями проверки. Поэтому «знаю школьный курс» не равно «готов к ЕГЭ»: нужно уметь быстро применять знания в нестандартных условиях и оформлять решения по требованиям экспертов.
Чтобы не потерять баллы на пробелах и невнимательности, нужна плановая подготовка: диагностика текущего уровня, выбор цели по баллам и список тем, которые придётся подтянуть именно в формате ЕГЭ, а не по ощущениям «я это когда‑то проходил».
Базовый и профильный уровни
Базовый уровень нужен для аттестата и поступления на специальности, где математика не профильный предмет. Профильный уровень используют вузы для отбора на инженерные, ИТ‑, экономические и многие естественно‑научные направления, поэтому к нему предъявляют более жёсткие требования по решению задач и оформлению.
| База | Профиль |
|---|---|
| Цель — подтвердить освоение школьного минимума и получить аттестат. | Цель — ранжировать абитуриентов по уровню владения математикой. |
| Задания проще, без сложной второй части. | Есть первая и вторая части, задачи повышенной и высокой сложности. |
| Подходит для гуманитарных и творческих направлений. | Требуется на технических, ИТ‑, экономических и смежных специальностях. |
Выпускник может выбрать только профиль и не сдавать базу: результат профильного ЕГЭ засчитывают и как подтверждение математики для аттестата, и как вступительный экзамен при поступлении.
Формат профильного ЕГЭ и система баллов
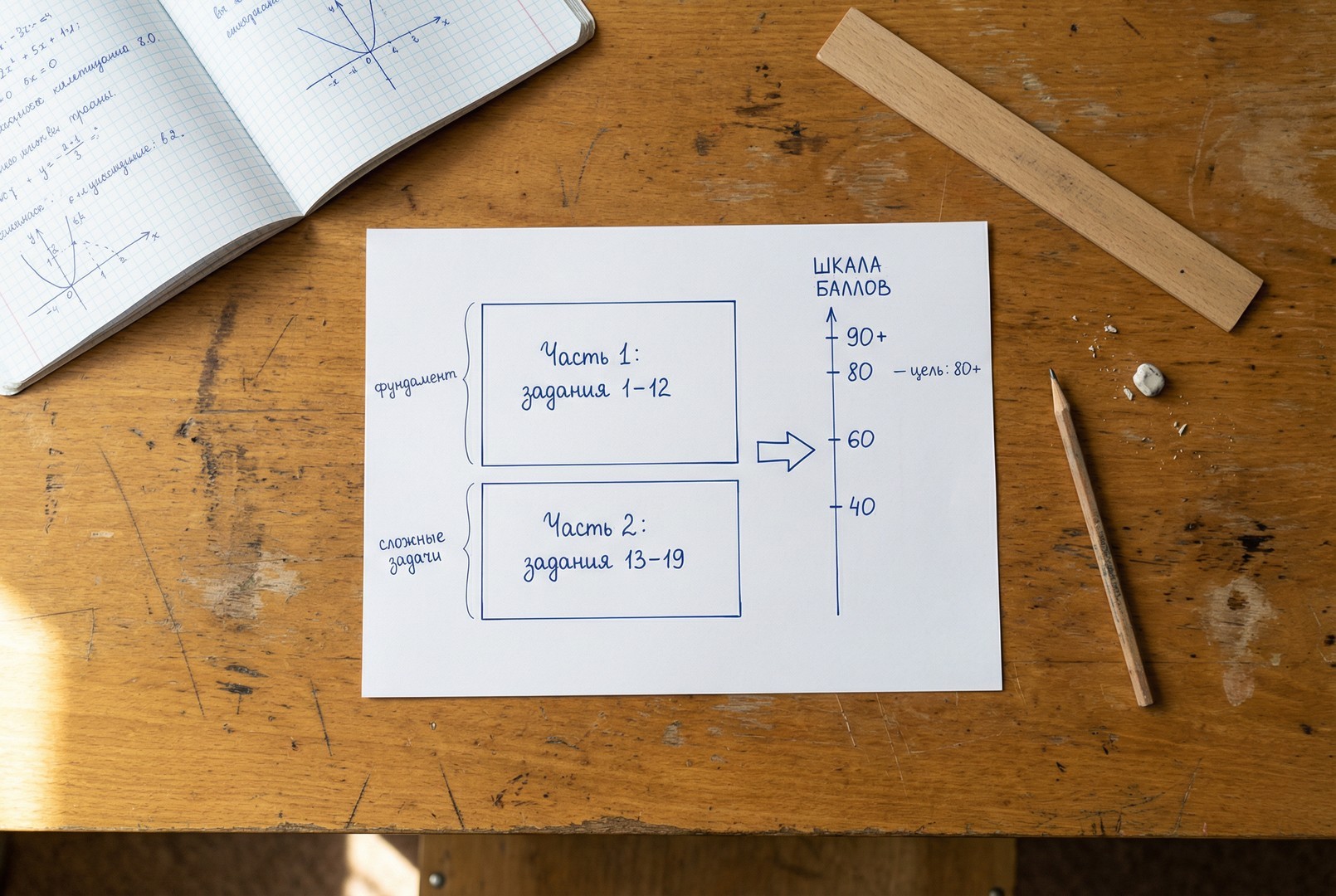
Профильный ЕГЭ по математике длится 3 часа 55 минут. Вариант делится на две части: первая содержит короткие задачи с числовым ответом, вторая — развернутые задачи, где нужно полное решение. Калькулятор использовать нельзя, поэтому важны устный счёт и аккуратные вычисления.
Понимание структуры помогает распределить силы: первая часть даёт стабильный «фундамент» баллов, вторая позволяет выйти на 80–90+. От цели по баллам зависит, сколько времени закладывать на отработку сложных номеров и оформления решений.
Структура экзамена
В профильном варианте 19 заданий. Номера 1–12 относятся к первой части, ответы записываются в виде числа. Номера 13–19 — вторая часть, где проверяют ход решения и обоснования. За каждое задание дают фиксированное число первичных баллов.
| Номер | Кратко тема | Тип ответа | Максимум первичных баллов |
|---|---|---|---|
| 1 | Арифметика, проценты | Краткий числовой ответ | 1 |
| 2 | Простые уравнения | Краткий числовой ответ | 1 |
| 3 | Текстовые задачи | Краткий числовой ответ | 1 |
| 4 | Прогрессии | Краткий числовой ответ | 1 |
| 5 | Функции и графики | Краткий числовой ответ | 1 |
| 6 | Геометрия на плоскости | Краткий числовой ответ | 1 |
| 7 | Стереометрия | Краткий числовой ответ | 1 |
| 8 | Неравенства и системы | Краткий числовой ответ | 1 |
| 9 | Вероятность и статистика | Краткий числовой ответ | 1 |
| 10 | Сложные текстовые модели | Краткий числовой ответ | 1 |
| 11 | Функции, производная | Краткий числовой ответ | 1 |
| 12 | Комбинированная задача | Краткий числовой ответ | 1 |
| 13 | Уравнение (часто тригонометрическое) | Развернутое решение | 2 |
| 14–16 | Геометрия и стереометрия | Развернутое решение | 2–3 |
| 17 | Текстовая задача повышенной сложности | Развернутое решение | 3 |
| 18–19 | Параметры и нестандартные задачи | Развернутое решение | 3–4 |
Как считают баллы и пороги
За задачи начисляют первичные баллы, затем их переводят в тестовые по шкале года проведения экзамена. Минимальный порог для аттестата по профилю обычно около 27 тестовых баллов, для поступления на многие технические и экономические направления — 50–60 и выше, на топовые программы — 70–80+. Ориентиры по шкале: примерно 35–40 тестовых соответствуют уверенной первой части без второй, около 60 — первой части плюс 1–2 задачи второй, 80 — нескольким устойчивым номерам второй части, 90+ — почти безошибочной первой и 3–4 сложным задачам. Чёткая цель по тестовым баллам позволяет решить, достаточно ли безошибочной первой части или нужно стабильно брать несколько задач второй части.
С чего начать: первый пробник и выбор цели по баллам
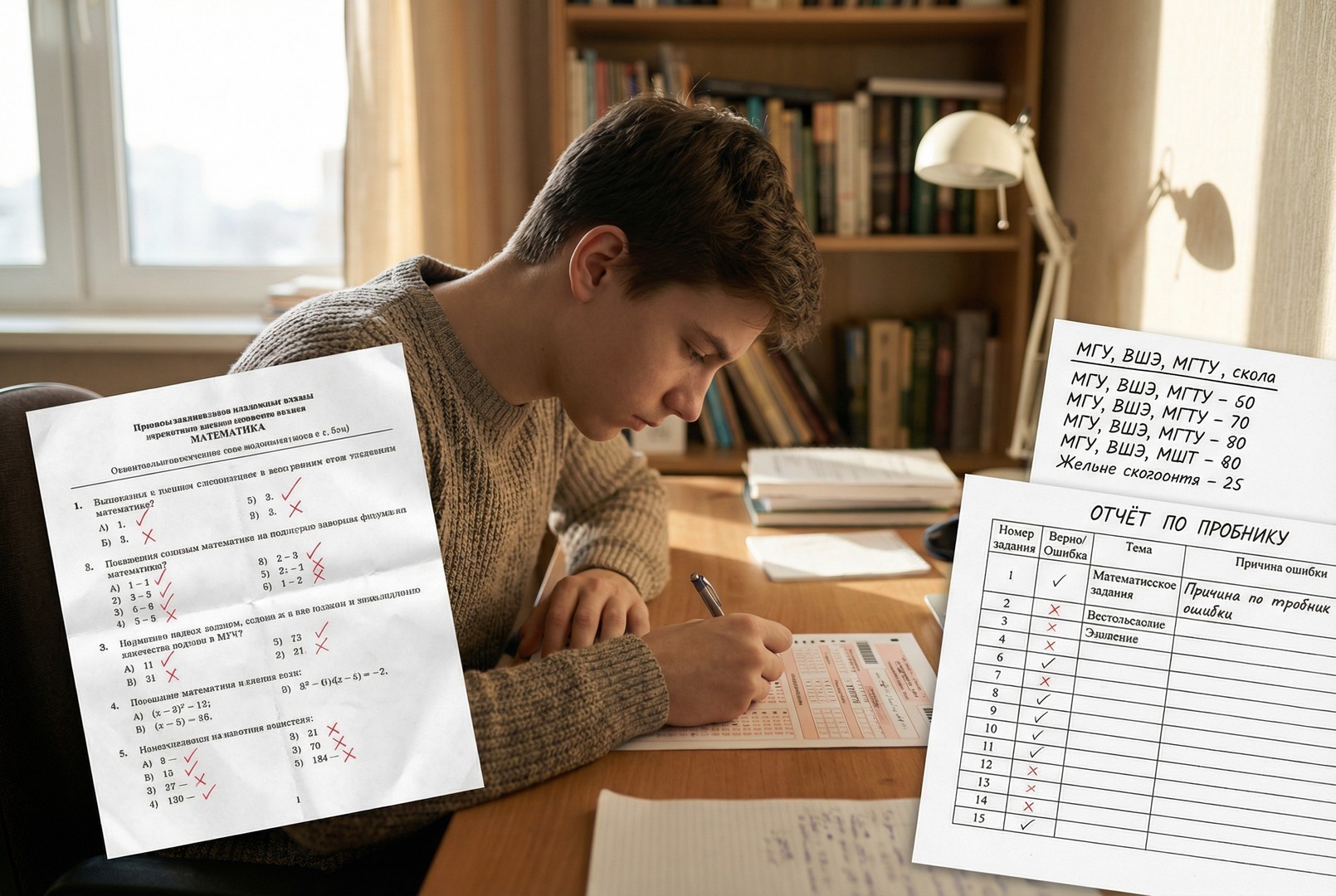
Старт без диагностики даёт ложное ощущение прогресса: можно месяцами решать задачи и не двигаться к нужному результату. Первый пробник показывает реальный уровень, слабые темы и даёт основу для плана: какие разделы тянуть в первую очередь и сколько задач второй части включать в цель.
Работает только честный формат: один вариант, ограничение по времени, без калькулятора и подсказок. После проверки важно не оценивать себя эмоционально, а разобрать, какие номера не получились и почему: не знал теорию, не успел, ошибся в вычислениях.
Низкий балл на старте — не приговор. Он показывает объём работы и помогает выбрать реалистичную цель: где достаточно безошибочной первой части, а где придётся стабильно решать 13, 15, 17‑е задачи и, возможно, одну из сложных геометрических.
Первый пробник по уму
Подойдёт демоверсия или вариант в формате ЕГЭ. Нужны тишина, 3 часа 55 минут, бланки или их аналог, запрет на интернет и сборники с решениями. Цель — смоделировать условия экзамена и увидеть, сколько задач реально удаётся решить за отведённое время.
- Отметить, какие номера решены верно, какие пропущены, где допущены вычислительные ошибки.
- Сгруппировать провалы по темам: уравнения, функции, геометрия, текстовые задачи, вероятность.
- Зафиксировать время: сколько ушло на первую часть, сколько — на каждую задачу второй.
- Выделить 2–3 самых слабых блока — они войдут в приоритетный план.
- Отдельно записать типичные ошибки: невнимательность, неверный формат ответа, спешка.
Как выбрать цель по баллам
Цель зависит от трёх параметров: текущего тестового балла, месяцев до экзамена и проходных баллов в выбранных вузах. При низком старте и небольшом сроке разумно нацелиться на уверенную первую часть и одну задачу второй. При среднем уровне и годе подготовки можно планировать 70+ с опорой на 13, 15, 17‑е номера.
| Текущий балл | Реалистичная цель | Упор в первой части | Минимум второй части |
|---|---|---|---|
| до 30 | 40–60 | Безошибочно 1–12 | 1 любая задача |
| 30–50 | 60–80 | Быстро и точно 1–12 | 13 и 17 либо 15 |
| 50+ | 80–90+ | Минимум времени на 1–12 | 13, 15, 17 и одна из 14, 16, 18 |
Чёткая цель задаёт стратегию: сколько часов в неделю уходят на базовые темы, а сколько — на отработку выбранных задач второй части и оформление решений.
План подготовки по времени: год, полгода, 2–3 месяца
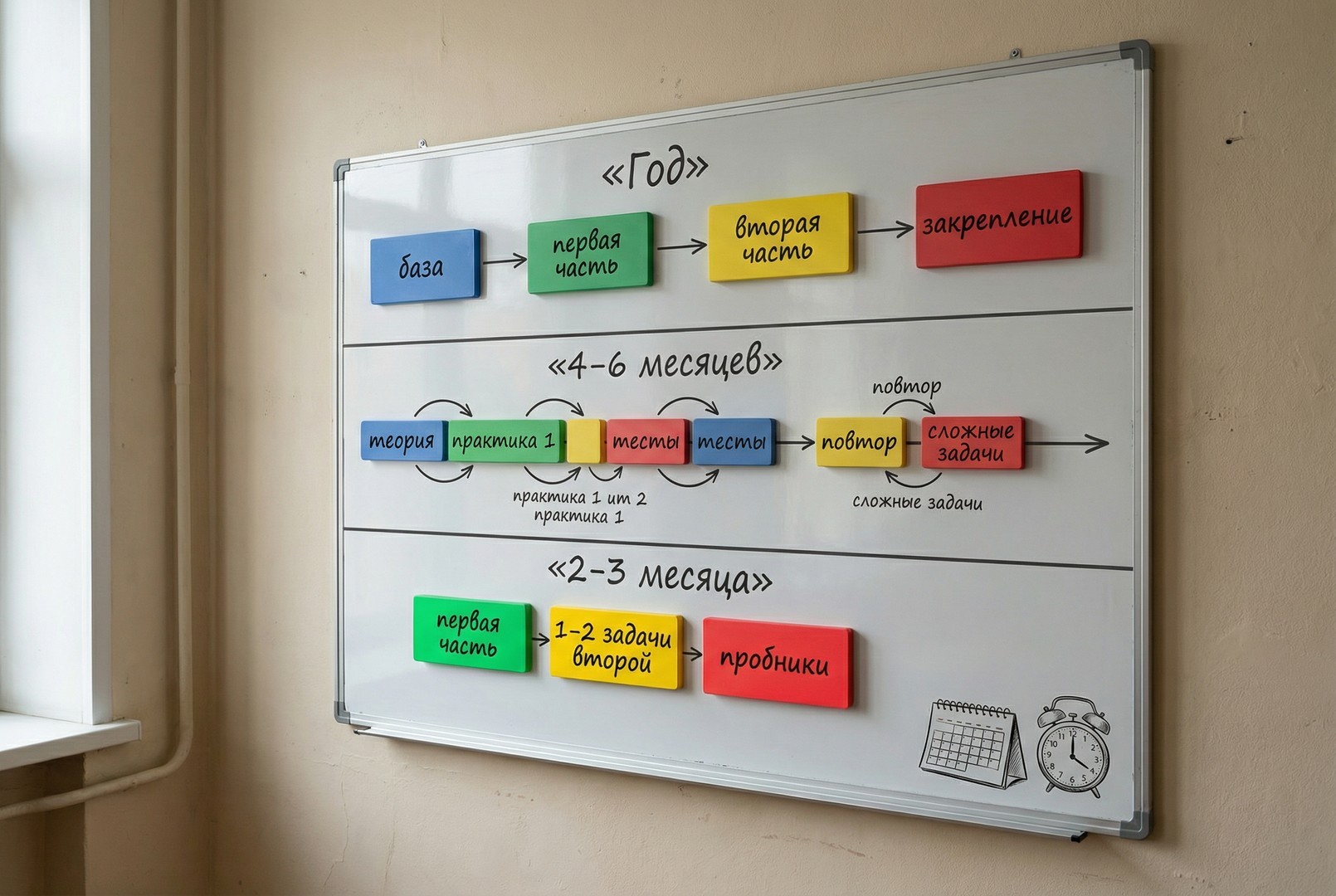
Срок до экзамена задаёт ритм. В любом сценарии работает один цикл: короткая теория по теме, серия задач, разбор ошибок и повтор через 1–2 недели. Пробники стоит писать регулярно, чтобы отслеживать рост баллов и корректировать план.
Если до экзамена год
Год позволяет идти по этапам и без перегрузки. Удобно разбить подготовку на четыре блока по 2–3 месяца.
- 1–2 месяц: повтор арифметики, процентов, уравнений, простых текстовых задач, старт геометрии.
- 3–5 месяц: вся первая часть, функции и графики, базовая стереометрия, первые задачи 13 и 17.
- 6–8 месяц: тригонометрия, неравенства, отработка 13, 15, 17, знакомство с 14 или 16.
- 9–10 месяц: закрепление выбранных задач второй части, работа над скоростью и оформлением.
Пробник раз в 4 недели, одна неделя в четверть — облегчённая: меньше новых тем, больше повторения, чтобы не выгореть.
Если осталось четыре-шесть месяцев
При полугоде приоритет — надёжная первая часть и «обязательный минимум» второй.
- 1–2 месяц: закрыть пробелы в базовой алгебре и геометрии, довести 1–12 до 80–90% верных.
- 3–4 месяц: целенаправленно отрабатывать 13 и 17, при хорошем уровне добавить 15.
- 5–6 месяц: чередовать варианты целиком и точечную работу по слабым темам.
Пробники раз в 2–3 недели. Сложные 18–19‑е задачи можно не брать, если цель до 80 баллов.
Если осталось два-три месяца
Короткий срок требует жёсткого отбора тем. Цель — максимум баллов за типовые задания.
- Неделя 1–2: довести первую часть до стабильного результата, выучить формулы, отработать формат ответов.
- Неделя 3–4: выбрать 1–2 посильные задачи второй части (обычно 13 и 17) и решать их по блокам.
- Последние недели: через день решать варианты с таймером, разбирать только ошибки, повторять формулы и шаблоны решений.
Пробник раз в неделю, без новой сложной теории — только закрепление и скорость.
Тематический каркас: какие темы нужны для 60–70 и 80+ баллов
Цель тематического плана — закрыть все типовые задания и не тратить время на лишнюю теорию. Удобно делить подготовку на блоки: алгебра и текстовые задачи, геометрия и стереометрия, функции и графики, тригонометрия, вероятность и статистика.
Для 60–70 баллов достаточно уверенно решать первую часть и 1–2 задачи второй: базовую алгебру, простую геометрию, текстовые задачи, элементы функций и вероятности. Для 80+ баллов нужен расширенный уровень: тригонометрия, производная, стереометрия, более сложные текстовые и экономические задачи.
| Раздел | Подтемы | Приоритет 60–70 | Приоритет 80+ |
|---|---|---|---|
| Алгебра и текстовые | Уравнения, неравенства, системы, проценты, прогрессии | Обязателен | Обязателен, плюс усложнённые модели |
| Геометрия и стереометрия | Площади, подобие, объёмы простых тел | Базовый уровень | Расширенный, задачи второй части |
| Функции и графики | Свойства функций, чтение графиков | Средний приоритет | Высокий, с производной |
| Тригонометрия | Основные формулы, уравнения | По минимуму | Полноценный блок |
| Вероятность и статистика | Классические модели, диаграммы | Обязателен | Обязателен |
Базовые алгебраические темы
Алгебра даёт большую часть баллов первой части и опору для задач 13 и 15. Сюда входят линейные и квадратные уравнения, простые рациональные и иррациональные уравнения, неравенства, системы, пропорции, проценты, прогрессии, текстовые задачи на движение, работу, смеси.
Рационально идти от простого к сложному: сначала арифметика и проценты, затем линейные модели и пропорции, после — квадратные уравнения и прогрессии, в конце — неравенства и системы. По каждой подтеме нужен цикл: краткая теория, серия однотипных задач, разбор ошибок, повтор через 1–2 недели.
Типовые номера профильного ЕГЭ, которые опираются на эти темы: задания на проценты и пропорции, текстовые задачи, прогрессии, простые уравнения и неравенства, экономические модели в 17‑м. При цели 80+ стоит добавить отработку логарифмов и более сложных рациональных выражений, если они входят в актуальные варианты.
Геометрия и стереометрия минимум
Геометрический минимум включает свойства треугольников и четырёхугольников, признаки и признаки подобия, окружность и углы, площади фигур, длины отрезков, элементы вектора и координат. В стереометрии важны призмы, пирамиды, цилиндр, конус, шар, их площади поверхностей и объёмы.
Работа с чертежом критична: аккуратный рисунок, обозначения всех данных, выделение искомых элементов, проверка, что чертёж не противоречит условию. Полезно тренировать перевод текста задачи в схему, особенно для стереометрии и задач с несколькими плоскостями.
Если геометрия слабая, при цели 60–70 баллов разумно сосредоточиться на базовых задачах первой части и одной посильной задаче второй (например, 14 или 16 по простым конфигурациям). Для 80+ баллов нужен системный курс: теоремы, стандартные конструкции, отработка планиметрии и стереометрии второй части.
Функции, тригонометрия, вероятность
Блок функций включает чтение графиков, нахождение значений по графику, монотонность, экстремумы, простые преобразования. На уровне ЕГЭ часто встречаются задачи на интерпретацию графиков реальных процессов и анализ кусочно-заданных функций.
Тригонометрия даёт базу для уравнений и неравенств второй части. Нужны определения синуса, косинуса, тангенса, основные тождества, формулы приведения, простые тригонометрические уравнения и умение работать с окружностью единичного радиуса.
Вероятность и статистика охватывают классические модели (равновероятные исходы, сочетания), условную вероятность на простых примерах, а также чтение таблиц, диаграмм и работа с выборками. Эти темы дают устойчивые баллы в первой части и встречаются в задачах на анализ данных.
Как готовиться к первой части (задания 1–12)
Цель первой части — набрать стабильные баллы за счёт отработанных шаблонов. Эти задания проверяют базовую алгебру, геометрию, текстовые задачи, функции и элементы вероятности, поэтому важно решать их быстро и без грубых ошибок.
Эффективнее тренироваться по темам. Сначала выбирается один блок (например, проценты или прогрессии), повторяется краткая теория, затем решается серия однотипных задач с постепенным усложнением. После каждой серии фиксируются ошибки и причины: невнимательность, пробел в формуле, непонимание условия.
Контроль времени обязателен. На первую часть стоит ориентироваться на 30–40 минут, поэтому при тренировке полезно ставить таймер и записывать, какие номера «зависают». Отдельно тренируются именно медленные задачи, пока они не начнут укладываться в нужный лимит.
- Чётко знать формулы и стандартные приёмы для своих типов задач.
- Решать минимум 3–4 полноценных варианта в неделю с акцентом на первую часть.
- Регулярно возвращаться к темам, где ошибки повторяются.
Типы задач и отработка первой части
В первой части встречаются блоки: арифметика и проценты, простые уравнения и неравенства, текстовые задачи, элементы геометрии и стереометрии, функции и графики, вероятность и статистика. Каждый тип соответствует 1–2 номерам и имеет ограниченный набор моделей.
Рабочая схема отработки такова: берётся одна тема, повторяются нужные формулы и типовые шаги решения, затем решается пачка задач только этого вида (10–20 штук подряд). После разбора ошибок составляется краткий конспект: «как решать» и «на чём спотыкаюсь».
К смешанным вариантам стоит переходить, когда по отдельным темам доля верных решений держится на уровне 80–90%. Тогда тренировка идёт уже в формате «как на экзамене» с таймером и последующим разбором только ошибочных номеров.
Как не терять лёгкие баллы
Большая часть потерь в первой части связана не со сложностью, а с невнимательностью: неверное чтение условия, пропущенный знак, неправильное округление, запись ответа в неверном формате (дробь вместо десятичной и наоборот).
Полезно вести список типичных ошибок. В него попадают повторяющиеся промахи: забытый модуль, перепутанные единицы измерения, неверное построение графика. Перед каждым новым вариантом этот список просматривается как напоминание, на что смотреть особенно внимательно.
- После решения варианта делать быструю вторую проверку только по ответам и единицам измерения.
- Сверять формат ответа с требованием задания (целое число, десятичная дробь, отрезок).
- Пересчитывать хотя бы самые «дорогие» и сомнительные номера.
Как готовиться ко второй части (задания 13–19)
Вторая часть даёт много первичных баллов и резко поднимает итоговый результат. Задачи здесь разного типа и сложности, поэтому важно выбрать «свои» номера под цель: для 70–80 баллов обычно достаточно уверенно решать 1–2 задания второй части, для 80–90+ — 3–4 и больше.
Полезно заранее решить, какие номера осваивать в приоритете. При слабой геометрии упор делают на уравнения и экономические задачи, при сильной — добавляют планиметрию и стереометрию. Параметры и 19‑е задачи стоит брать только тем, кто уже стабильно закрывает первую часть и базовые номера второй.
Каждый выбранный номер отрабатывают по одной схеме: теория и разбор типовых методов, серия однотипных задач от простых к сложным, затем регулярное повторение. Отдельно тренируют оформление: полные выкладки, обоснования переходов, чёткие выводы, чтобы эксперт без догадок проследил ход решения.
Обзор и обязательный минимум второй части
Номера 13–19 различаются по теме и вкладу в балл. Таблица помогает расставить приоритеты под нужный результат.
| Номер | Тема | Баллы | Приоритет 70–80 | Приоритет 80–90+ |
|---|---|---|---|---|
| 13 | Тригонометрическое уравнение | 2 | Высокий | Высокий |
| 14 | Планиметрия | 2 | Средний | Высокий |
| 15 | Алгебраическое неравенство | 2 | Высокий | Высокий |
| 16 | Стереометрия | 3 | Низкий | Средний |
| 17 | Экономическая задача | 3 | Высокий | Высокий |
| 18 | Параметры | 4 | Низкий | Средний |
| 19 | Нестандартная задача | 4 | Низкий | Средний/высокий |
Минимальный набор для 70–80 баллов — 13, 15 и 17: у них устойчивые типы решений и хороший «выход» баллов. План освоения: сначала базовая теория и разбор 5–10 простых задач по каждому номеру, затем регулярная практика по вариантам с фиксацией всех ошибок и доработкой слабых шагов.
Сложные задачи и оформление решений
Геометрические задачи 14 и 16, параметры и 19‑е задания целесообразно брать, если цель 85+ и уже нет провалов в первой части и базовых номерах второй. При дефиците времени лучше довести до стабильности 13, 15, 17, чем распыляться на все типы сразу.
Оформление влияет на итоговый балл не меньше, чем идея решения. Эксперт должен видеть: план, обоснованные переходы, аккуратные чертежи, явный ответ. Помогает короткий чек‑лист: подписывать все обозначения, делать вывод после каждого ключевого шага, не пропускать вычисления «в уме», в конце отдельно выписывать окончательный ответ.
Формат подготовки и учебный ритм
Формат подготовки влияет на темп и результат. Важно выбрать способ, который подходит по уровню самодисциплины, бюджету и цели по баллам, а затем задать стабильный недельный ритм занятий. В среднем для профиля нужны 6–8 часов в неделю, чтобы выйти на 60–70 баллов, 8–10 часов — на 80+, 10–12 часов и больше — на 90+ при условии качественной работы.
Самостоятельно, с репетитором или на курсах
| Формат | Плюсы | Минусы | Кому подходит |
|---|---|---|---|
| Самостоятельно | Гибкий график, минимум затрат, можно двигаться в своём темпе | Нет внешнего контроля, риск пробелов в теории и хаотичного плана | Мотивированным, кто умеет планировать и уже набирает 50+ баллов |
| Репетитор | Индивидуальный темп, разбор именно ваших ошибок, быстрый фидбек | Дорого, зависимость от расписания, результат падает без домашней работы | Тем, у кого база слабая, цель 80+ или сложно учиться самому |
| Курсы | Структурированная программа, системные домашние задания, атмосфера группы | Меньше индивидуальной работы, фиксированное расписание | Нужен план и мотивация, но бюджет ограничен по сравнению с репетитором |
При ограниченном бюджете часто комбинируют форматы: базу и первую часть закрывают по курсам или самостоятельно, а сложные темы второй части разбирают точечно с репетитором раз в 1–2 недели.
Пример учебной недели, формульник и дневник ошибок
Оптимальная нагрузка для профиля — 6–10 часов в неделю: 3–4 занятия по 1,5–2 часа. Часть времени уходит на теорию, остальное — на задачи и разбор ошибок.
Пример недели: 2 дня — алгебра и первая часть, 1 день — геометрия, 1 день — вторая часть. Раз в 2–3 недели добавляют пробник «как на экзамене» с последующим разбором.
Формульник ведут в отдельной тетради: ключевые формулы по темам, краткие примеры их применения, пометки о типичных ловушках. К нему регулярно возвращаются перед решением задач.
Дневник ошибок помогает не повторять одни и те же промахи. В него записывают номер задачи, суть ошибки, верное решение и короткий вывод, что изменить в подходе. Раз в неделю полезно просматривать записи и решать по 2–3 похожие задачи на каждую частую ошибку.
Подготовка с нуля и финиш перед экзаменом
Под слабой базой понимают пробелы в арифметике, уравнениях, простых текстовых задачах и почти полное отсутствие геометрии. В такой ситуации цель и план зависят от срока до ЕГЭ.
Как готовиться к ЕГЭ по математике с нуля
При старте «с нуля» обычно сохраняются навыки устного счёта до простых примеров и базовые формулы площади прямоугольника, но нет уверенности в дробях, процентах, пропорциях, линейных и квадратных уравнениях, прогрессиях и элементарной геометрии.
Первый этап — арифметика и текстовые задачи: действия с дробями, проценты, пропорции, задачи на скорость, работу, смесь, простые финансовые сюжеты. Эти темы закрывают значительную часть первой части и дают быстрый рост баллов.
Второй этап — уравнения, неравенства, системы и прогрессии. Нужен минимум: линейные и квадратные уравнения, простые рациональные выражения, арифметическая и геометрическая прогрессии, базовые задачи на них.
Геометрию до рабочего минимума подтягивают через опорные блоки: треугольники и подобие, окружность, площади фигур, объёмы призмы и цилиндра, построение аккуратного чертежа. Для слабой базы достаточно уверенно решать типовые задачи первой части и простые планиметрические номера.
Реалистичный потолок: при годе системной работы можно выйти на 70–80 баллов, при 6 месяцах — на 60–70, при 3 месяцах — на 50–60 с упором на первую часть и 1–2 задачи второй.
Последние месяцы и день экзамена
За 1–2 месяца основной акцент смещается на пробники и повторение. Оптимально писать вариант раз в 1–2 недели по полному времени, затем разбирать каждую ошибку и заносить её в дневник с последующей отработкой похожих задач.
Новый материал в этот период добавляют точечно: только то, что даёт быстрый прирост баллов и опирается на уже освоенную базу. Остальное время уходит на закрепление сильных тем и доведение первой части до стабильного результата.
- Нормализовать сон: не менее 7–8 часов, без ночных «забегов» перед пробниками.
- Делать короткие ежедневные сессии по 30–60 минут вместо редких марафонов.
- Оставлять 1 выходной в неделю без математики для восстановления.
В день экзамена полезно заранее решить, в каком порядке выполнять задания (обычно сначала вся первая часть, затем выбранные номера второй), сколько времени отводить на каждую часть и когда начинать проверку. За 10–15 минут до конца стоит пройтись по бланкам, сверить номера, формат ответов и особенно внимательно проверить задачи, где были частые ошибки на тренировках.
Ресурсы и литература для подготовки
Набор материалов лучше сразу ограничить: 2–3 основных источника и несколько дополнительных под задачи. Это снижает хаос и даёт стабильный прогресс.
Официальные материалы дают эталон формата и требований.
- Демоверсия профильного ЕГЭ по математике на сайте ФИПИ.
- Кодификатор и спецификация экзамена в разделе ЕГЭ по математике.
- Открытый банк заданий ФИПИ по математике.
Онлайн‑ресурсы помогают тренировать задачи в нужном объёме.
- РешуЕГЭ (math-ege.sdamgia.ru) — тренажёры по номерам и темам, варианты.
- Сайт Ларина с подборками сложных задач второй части.
- Онлайн‑платформы с автоматической проверкой ответов и статистикой ошибок.
Книги и сборники нужны как опорный курс.
- Сборники профильного ЕГЭ под ред. Ященко с разбивкой по номерам.
- Задачники по алгебре и геометрии авторов типа Мордковича, Атанасяна.
- Краткие теоретические конспекты и формульники по профильной математике.
Базу подготовки стоит строить на официальных материалах и одном удобном онлайн‑ресурсе, а книги и дополнительные сайты подключать точечно под слабые темы и вторую часть.
Краткий вывод и следующий шаг
Подготовка к профильному ЕГЭ по математике опирается на понимание формата: 19 заданий, первая часть на быстрый счёт и типовые модели, вторая — на развёрнутые решения и оформление. От цели по баллам зависит, какие номера второй части брать и сколько времени им отдавать.
Диагностика через пробники показывает стартовый уровень и слабые темы. По результатам удобно задать реалистичную цель по тестовым баллам и решить, нужен ли только самостоятельный режим или стоит подключить репетитора либо курс.
Дальше нужен план: по времени (год, полгода, 2–3 месяца), по темам (алгебра, геометрия, функции, тригонометрия, вероятность) и по частям экзамена. Первая часть должна стать почти безошибочной, вторая — давать стабильный «минимум» под выбранную цель.
Простой следующий шаг: решить один вариант в формате ЕГЭ, посчитать баллы, выписать провальные темы и по ним составить таблицу «неделя → темы → количество задач». Такой личный план уже можно заполнять пробниками и регулярным разбором ошибок.